NUMBER: THE CONNECTING PATTERN OF EUROPEAN-DERIVED AUSTRALIAN LIFE
English-speaking mothers and fathers teach their babies the number names, counting pegs or people or pieces of toast. They riddle, they chant and they sing: 'One, two, three, four, five. Once I caught a fish alive .. .'. In school, learning the number names and how to use them becomes a central activity of the child's day. Counting money, telling time, following a recipe-the number system mediates all but the most intimate of human relations in the Western world. Numbers can be put on just about anything, and so give whatever it is that is being talked about a specific value. Using its value, people understand something of where it fits into the scheme of things.
In its most basic sense, a number series is a linguistic pattern that enables one to count or to add up separate things, encoding the practice of tallying on fingers. It might be considered a kind of 'linguistic trick' that provides a means of counting beyond ten. Numerals constitute an infinite series by having a base about which repetition occurs and rules by which any element may be derived from the element which precedes it. Decimal number systems associated with Indo-European languages have ten as their base unit. Thus, in a decimal system, ten is the point in the series which marks the end of the basic set of numerals. As each ten is reached, the basic series is started again. Other cultures have used other base units like duodecimal (base twelve) or vigesimal (base twenty).
One instinctively understands the use of fingers and toes for tally-keeping in a nonlinguistic way. One separated finger codes for one separated item, indicating, perhaps, the passing of a sheep through a gate or the filling of a vessel with grain. But if we then extend the coding operation and say a word which codes for the finger or toe, we have done something much more complex and much more useful. In saying a word as a finger is held up, we understand that the word does not name either the item, or the finger. It names a position in a progression. Thus, numerals, or number names, are a linguistic code with which we may record how far through the series of fingers and toes we have progressed, and how many times we have done it.
Notions of equivalence and hierarchy (and many other notions as well) are enabled through the system of number names. Each succeeding number has a higher value than all antecedent numbers. The number system encompasses Western life. Though it carries the appearance of utter neutrality, it also seems to fit 'naturally' with notions of economic hierarchy and competition over value. The working of the number system carries a powerful ideology: a particular image of orderliness across space and time which lends itself to particular political and economic ends. Imagine, for example, what it might mean to build capitalism in a culture in which kinship took precedence over number.
Many, perhaps most, everyday transactions in Western industrial society require the use of the number system:
'I didn't get up till twenty past eight this morning, so 1 was half an hour late for work.'
'Turn left at the second light, about a hundred metres down the road, the tax office is in the third building on your right, fifth floor.'
'One box of cereal – ninety-eight, chicken soup – two for one dollar, three hundred grams of hamburger – two fifty; that comes to four forty-eight; change of ten; four fifty, five, and five is ten.'
'Uncle Joe sold off the the back paddock. It's been subdivided into half-acre blocks, going for fifty thousand each.'
The apparent triviality of the examples above is an indication of how much the number system is taken for granted. The first case shows that everyday life is minutely divided into mathematical cycles which are themselves numerically related to lunar (monthly) cycles and solar (annual) cycles. The second case shows the spatial grid which (as we shall see in the next exhibit) is conceived of as covering the planet and, at least in cities, is also extended vertically in a precise numeric way. The third case shows, in everyday life, both the complexity and power of the number system as applied to trade. In a bartering system, such a transaction might have taken hours to negotiate and involved far richer and more intricate social interactions. The cereal would have been grain from the fields and the beef, an animal, thus ensuring that both parties to the transaction had some particular knowledge of the natural world, utterly unnecessary to a supermarket employee and customer. The final example (which will also be amplified in the next exhibit) shows how the land itself, to a significant degree, is understood in terms of numeric cycles: length and width establishing area within selected boundaries, and the market establishing monetary value.
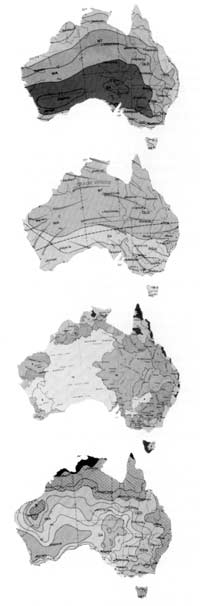
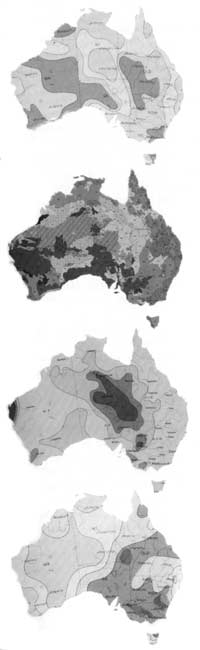
4.2
These maps depict numerical averages relating to diverse natural features such as annual runoff of surface water, vegetation coverage by botanical classification, annual temperature range, sunshine and cloud cover, seasonal wind patterns and even bushfires and duststorms.
Learning to count comes first, then the Western child learns to measure: to give numeric value to parts of things, and to subdivide 'the flowing face of nature' into arbitrary units which can be counted. Thus, the notion of size is made exact by developing concepts, or qualities, such as length, width, area and volume. Again, these concepts are so taken for granted that adults tend to assume them to be qualities of nature itself, rather than conceptual tools which society has developed for talking about and manipulating the natural world. It is primary school teachers in contemporary Western society who must regularly explain what these qualities actually mean. They are wise enough to teach children to understand things like length by asking them to carry out the practices employed when numbers are put on length (that is, giving them a ruler and setting them to measuring). The qualities themselves are elusive and mysterious things, and so they are objectified and naturalised. Though not 'facts of nature', they are what we might call 'social facts'. They are used in good faith by Westerners as 'real things' to construe the natural world as so divided.
Obviously it is easier to integrate numbers, counting and measuring into the social scheme of things if the ordinary language that people use has them focusing on spatially individuated things, as we saw English doing in Exhibit 2. In this situation, counting seems to follow naturally from talking. This leads us on to the question of 'natural kind', which we also considered earlier. Part of using the number system is deciding to what units numbers should be applied; the decision must be made as to precisely what to count, and what constitutes a unit in measuring.
In Exhibit 2 we considered some of the conceptual problems associated with the questions of where to draw lines and how to establish natural categories within nature. Some types of things in nature are much more amenable to quantification than others. For example, it is much easier to assign numeric value to trees and to the board feet of timber they contain than it is to put numbers onto the complex ecological relationships which those trees sustain. Furthermore, a monetary value can immediately be placed on cut timber so measured, whereas we have not yet learned to measure the monetary loss in terms of land degradation, long-term job loss, tourist amenity, cultural equilibrium and ecological health. This is only one well-known example of how our choice of what to quantify in nature has a direct and often devastating impact on our lives and those of our children, on our culture and on nature itself. It shows how the use of number conjures up the notion of value in a particular way.
We have seen how the number system constitutes one kind of grid which can be 'placed over' the lumpy, bumpy landscape and make that landscape easier for people to deal with and control. Numbers mediate our involvement with the world, and their use is intimately tied up with the power and remarkable achievement of modern industrial society. But using numbers is helpful in specific sorts of ways. For example when numbers are used in statistical ways, as they have been used to assemble the maps in ITEM 4.2, vast ideas can be precisely conveyed. Yet at the same time something is lost.
Let's assume you are somewhere in Australia on a particular day in the year, holding in your hand the grid maps of ITEM 4.2. You wish to predict the weather for the next few days; you wish to know what vegetation grows just over that rocky ridge; you wish to find fresh food. Maps of this sort-based on averages, on highly generalised calendrical cycles, focusing on particular variables but entirely ignoring others-such maps tell you virtually nothing about what you as an individual will actually find in the real world on that day. (Refer to Maps are territories, pp.19-27, for the distinction between indexical and non-indexical texts.) It is no exaggeration to say that a person skilled in bushcraft has no need whatever for these sorts of data, except perhaps to start a campfire. But at the same time let us not forget that for particular purposes they enable a land never visited to be known and controlled from a great distance. And that has profound implications for us all.
Knowledge which is superior for some purposes may be useless, possibly even counterproductive, for other purposes. The uses to which knowledge can be put are directly related to the conditions and assumptions of its production and the form in which it is communicated. The trick is to remember that knowledge, no matter how well dressed in number, is never value-free. This insight opens up the understanding that both of the knowledge systems coming together in ganma have their limitations and their uses.
We could not extricate number from Western culture, even should we wish to do so. Solving the problems which number has created in Western society is a twofold project: firstly, we must find ways of letting number speak forcefully for values other than monetary aggrandisement and short-term economic growth. Secondly, we must learn how to revitalise the values which are more readily understood and preserved within other ways of patterning knowledge, for example, the kinship system.